La biomécanique

En orthodontie, le traitement consiste à appliquer des forces sur les dents afin d’obtenir un déplacement dentaire en adéquation avec une réponse tissulaire optimale. Voici quelques notions à la base de la compréhension des concepts biomécaniques fondamentaux, nécessaire à celle des déplacements dentaires.

• La mécanique traditionnellement divisée en statique, cinématique et dynamique, est la partie de la physique qui étudie l’interaction entre les forces, la matière et le mouvement :

La statique étudie et définit les forces, ainsi que l’équilibre des systèmes matériels par rapport à un repère donné.

La cinématique étudie le mouvement en lui-même, sans égard aux forces qui les produisent.

La dynamique étudie le mouvement en fonction des causes qui lui donnent naissance.

• Un appareil d’orthodontie, en développant des forces et leurs moments, ajoute des composantes à l’équilibre des forces neuromusculaires. Il en résulte un déplacement des structures concernées, jusqu’à l’établissement d’un nouvel équilibre.

La mise en place d’un système de forces a des répercussions tridimensionnelles : ce sont les effets secondaires qu’il convient de connaître afin de les utiliser au mieux, ou de chercher à les prévenir si elles sont néfastes. On les découvre en utilisant le principe de l’action et de la réaction, et en matérialisant le diagramme des forces et moments en présence à l’équilibre.

C’est ainsi que chaque situation clinique est analysée, et c’est seulement dans un second temps que l’on choisit ou conçoit un type d’appareil, de ressort ou de boucle.

La biomécanique quant à elle, est une discipline qui tente de créer un lien harmonieux entre les sciences biologiques et les sciences physiques. En orthodontie, elle permet le passage du diagnostic à l’obtention des résultats thérapeutiques ; refuser son existence, c’est créer à ce niveau un hiatus particulièrement préjudiciable.

Si on demande à une technique orthodontique de traiter toujours de la même manière un syndrome donné, on aboutit à une conception qui tend à unifier tous les traitements : c’est une conduite sans prévision qui ne tient pas compte ni de la multiplicité des différentes étiologies ni de la grande variété des réponses.

NOTIONS FONDAMENTALES DE BIOMECANIQUE :

Enoncé des Lois de Newton :

– Première loi de Newton ou principe d’inertie : Tout corps persévère dans l’état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n’agisse sur lui, et ne le contraigne à changer d’état.

Autrement dit, s’il n’y a pas de force qui s’exerce sur un corps, ou si la somme des forces s’exerçant sur lui est égale à zéro, sa direction, son sens et sa vitesse ne changent pas ou, ce qui revient au même, son accélération est nulle.

– Deuxième loi de Newton ou Principe Fondamental de la Dynamique : Si la masse d’un corps est constante,

L’accélération subie par un corps de masse m est proportionnelle à la résultante des forces qu’il subit, et inversement proportionnelle à sa masse m.

Ainsi, la force nécessaire pour accélérer un objet est le produit de sa masse et de son accélération : plus la masse d’un objet est grande, plus grande est la force requise pour l’accélérer à une vitesse déterminée. Quelle que soit la masse d’un objet, toute force nette non-nulle qui lui est appliquée produit une accélération.

– Troisième loi de Newton ou principe d’action réciproque : Tout corps A exerçant une force sur un corps B subit une force d’intensité égale, mais de sens opposé, exercée par le corps B.

I-1) Les forces :

Selon LAMORLETTE, une force est définie comme toute cause capable de mettre en mouvement ou de changer la forme d’un corps.

Elle est caractérisée par :

• Son point d’application ou origine,
• Son module ou intensité (l’unité légale est le NEWTON, mais en orthodontie, le gramme et parfois le kilogramme sont utilisés.)
• Sa direction,
• Son sens ( une direction a 2 sens),

Tout cela définit un vecteur.

L’orthodontiste a souvent besoin de l’addition de plusieurs forces, aboutissant à un système que l’on peut parfois remplacer par sa résultante. Inversement une force peut être remplacée par ses composantes.

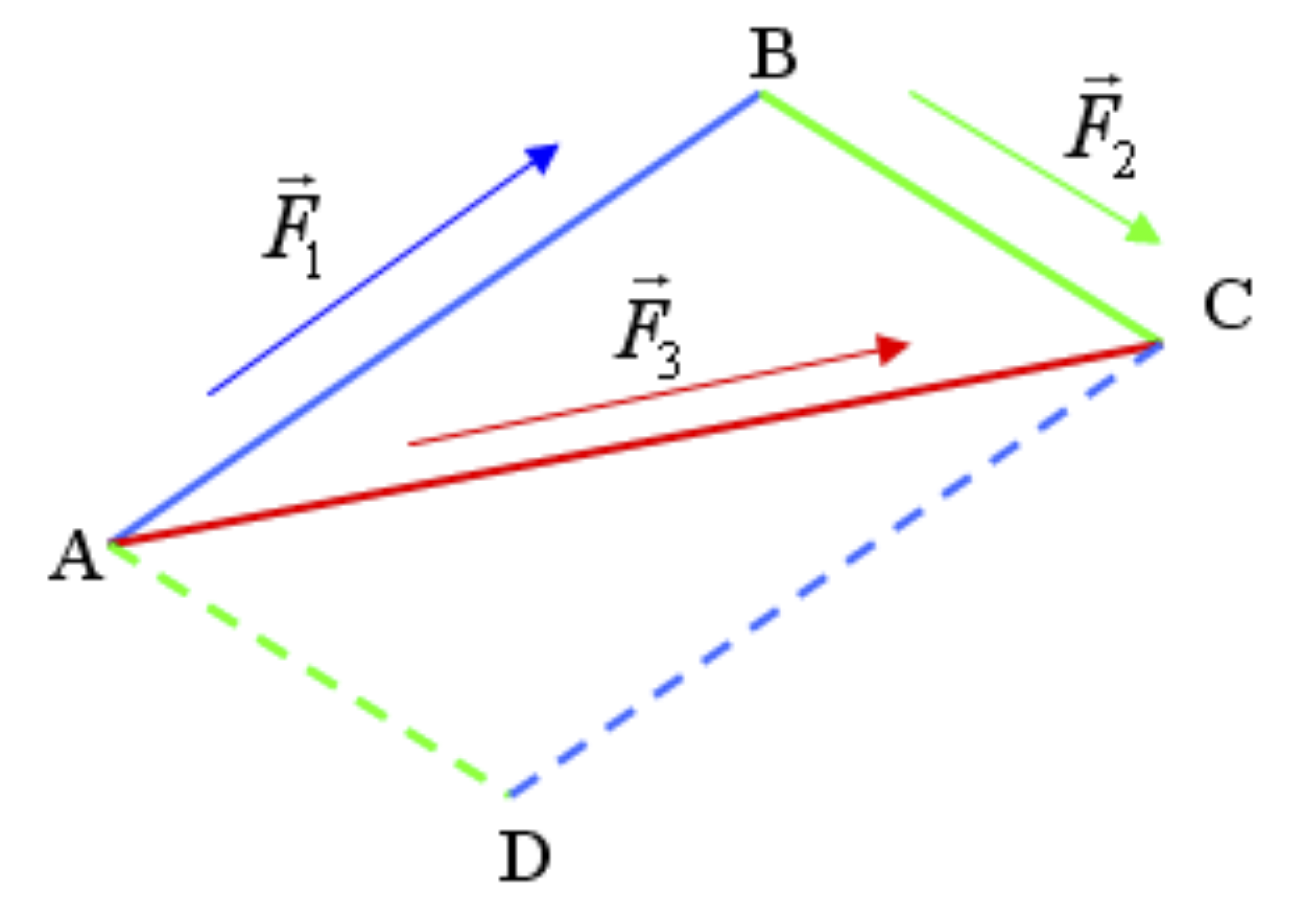
Fig. 1 Somme vectorielle : F3 = F1 + F2

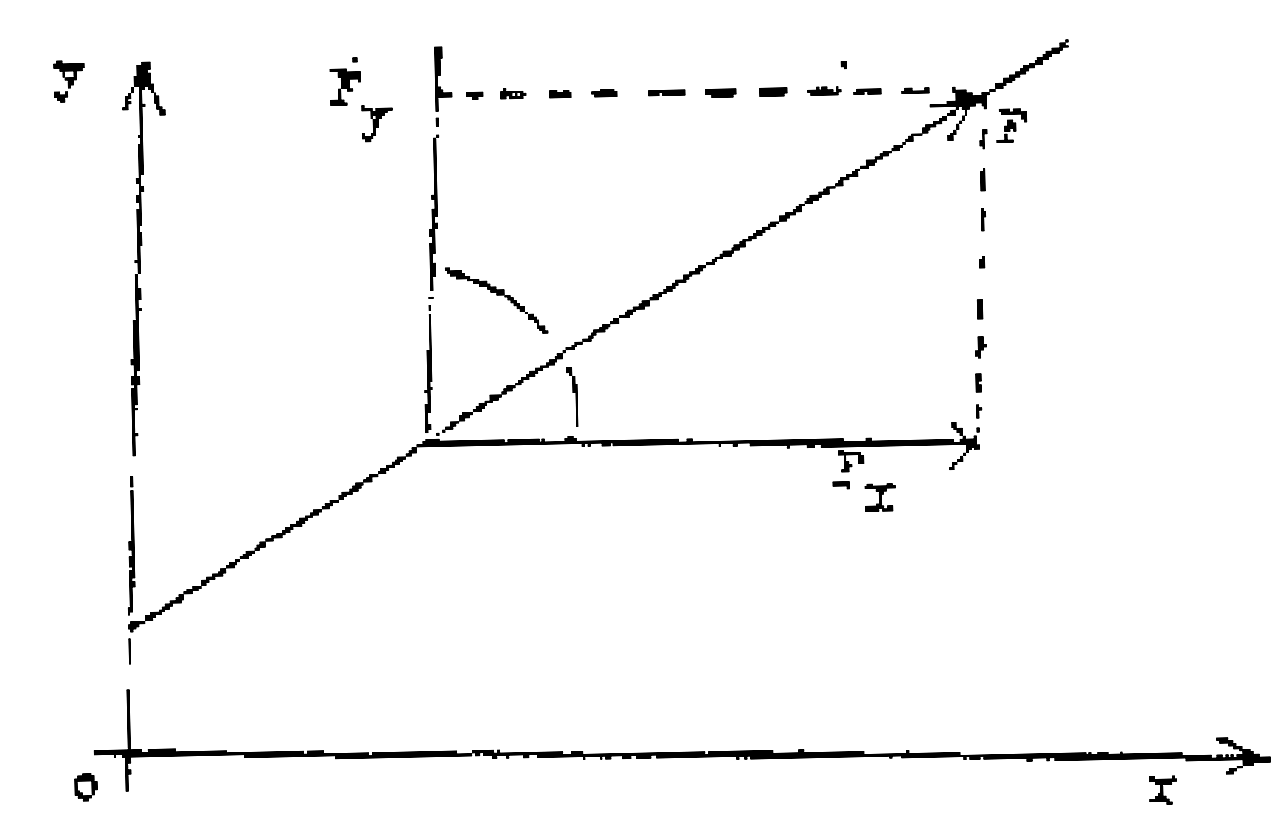
Fig. 2 Décomposition d’une force en deux composantes orthogonales d’après Larmolette

Tout corps A exerçant une force sur un corps B subit une force d’intensité égale, mais de sens opposé, exercé par le corps B : Action = – Réaction, de telle sorte qu’à l’équilibre, la somme des forces soit égale au vecteur nul.

En biomécanique orthodontique, il convient aussi de considérer la durée et le rythme d’application de la force, mais ces deux facteurs n’interviennent pas directement sur la mécanique proprement dite.

I-2) Le centre de résistance (CR)

Le centre de résistance est le point d’un solide par lequel il suffit de faire passer la ligne d’action d’une force d’intensité, de direction, de point d’application et de sens quelconque, pour obtenir une translation de ce solide.

Sa situation est indépendante du système de forces que l’on peut lui appliquer, sa localisation dépend à la fois de la dent, de sa forme et de sa composition mais également des propriétés du milieu qui l’entoure. Pour un solide isotrope dans un milieu isotrope, représente le centre géométrique de ce solide. Le milieu étant hétérogène, cavité buccale pour la couronne et os alvéolaire pour la racine, le centre de résistance est situé vers le milieu le plus dense, c’est-à-dire du côté apical (on le situe habituellement et par commodité sur l’axe de symétrie, au niveau du tiers apical de la racine des dents ou au niveau de la furcation des pluriradiculées).

Sa position dépend (BONNEFONT) :

• De la hauteur de l’os alvéolaire,
• De la surface radiculaire (fonction de la morphologie radiculaire),
• De la nature des structures parodontales (fonction de la densité de l’os alvéolaire, de l’élasticité des structures desmodontales).

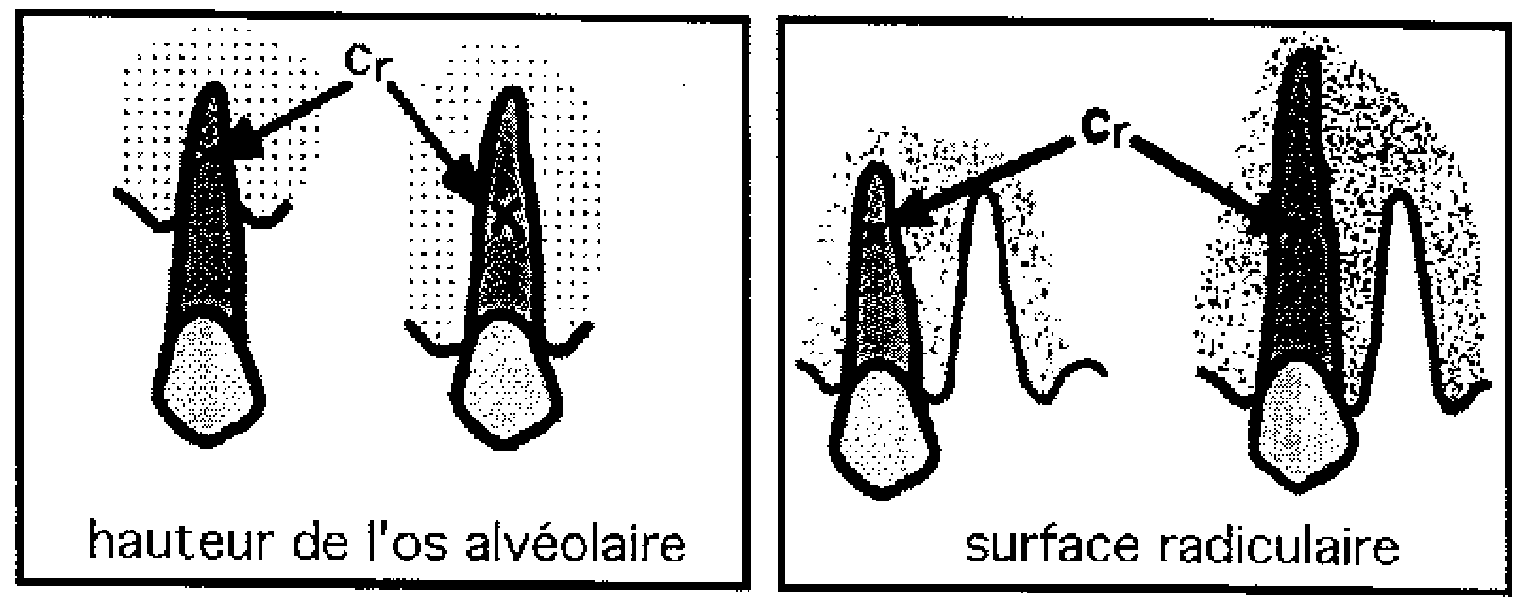
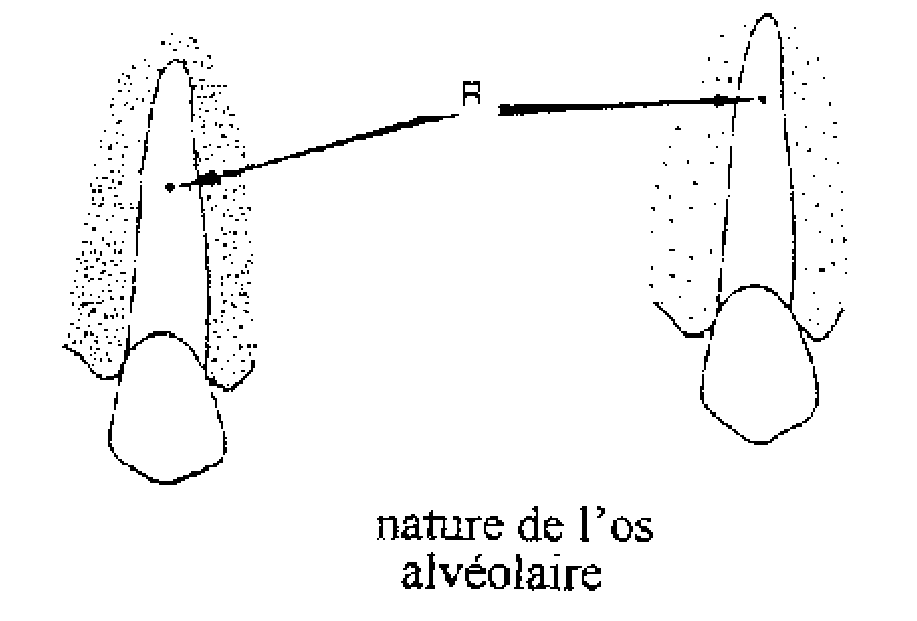
Fig. 3 Variation de la position du centre de résistance d’après Bonnefont

Fig 4.Situation du centre de résistance d’une monoradiculée dont le parodonte est sain d’après Burstone.

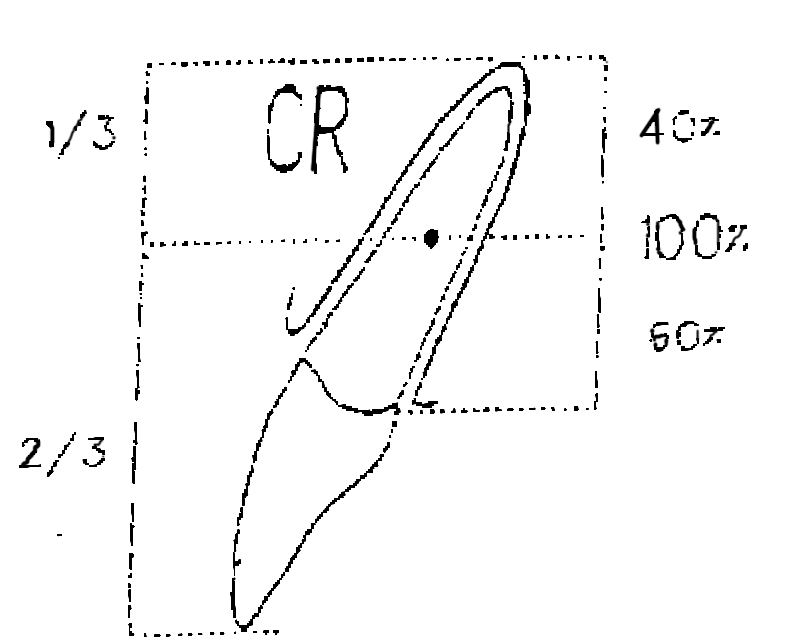
Pour un système dentaire C formé de plusieurs éléments, le centre de résistance sera plus proche de la dent à plus fort coefficient de résistance.

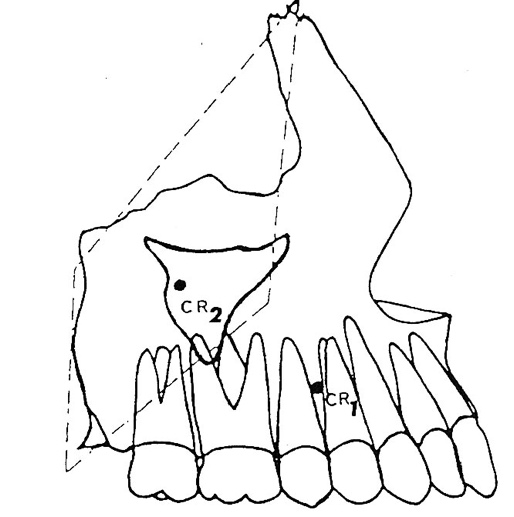
Les centres de résistances décrits par Teuscher :

CR1 : centre de résistance alvéolo-dentaire

CR2 : centre de résistance maxillaire

I-3) Le centre de rotation :

Une force ne passant pas par le centre de résistance provoque une combinaison de rotation et de translation. Cette combinaison représente un pivotement de tous les points de la dent autour du « centre de rotation ». A l’inverse du centre de résistance, il dépend uniquement du système de forces utilisé. Il n’est ni une propriété du corps, ni une propriété du milieu dans lequel il se trouve. Sa position par rapport au centre de résistance détermine le type de mouvement obtenu :

• S’il est éloigné de la dent, on obtient à l’extrême un mouvement de translation.
• S’il est confondu avec le centre de résistance, on obtient un mouvement de rotation pure.
• Entre ces deux positions extrêmes, on obtient des mouvements combinés de roto translation (DEMANGE)

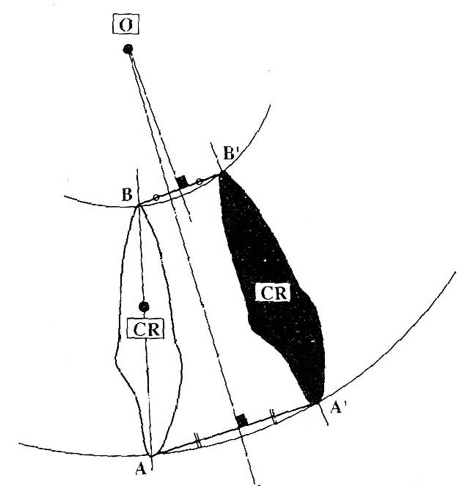
Fig. 4’ : le déplacement d’une dent peut toujours se résumer à un moment de rotation dont le centre 0 se trouve à l’intersection des médiatrices du déplacement A A’ et B B’ de deux points quelconques de cette dent ( GARCIA)

I-4) Le moment

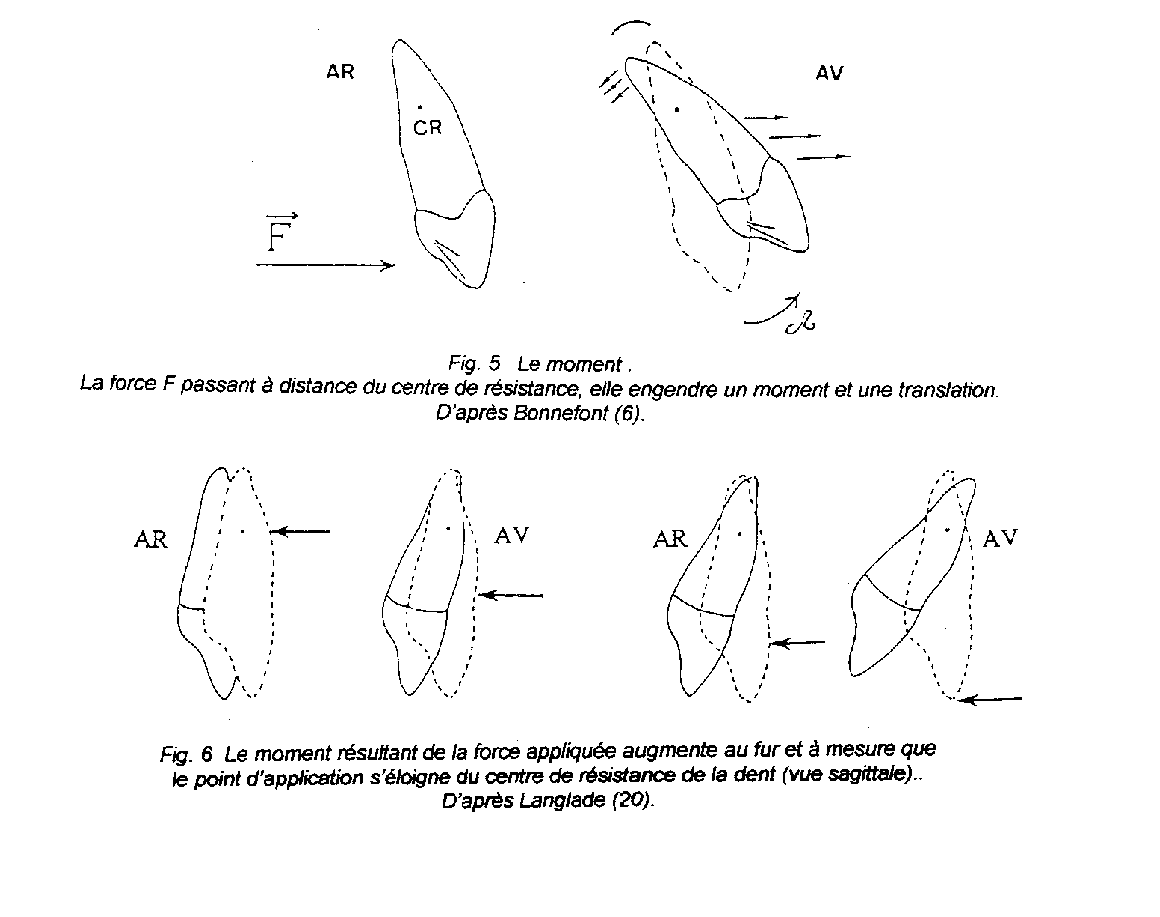
Quel que soit le niveau où l’on applique une contrainte, elle se trouve en tous points du mobile. Une force dont la ligne d’action ne passe pas par le centre de résistance d’un corps produit une rotation, qui se traduit au niveau de celui-ci par un moment. Son intensité est égale au produit de l’intensité de la force, par la distance perpendiculaire à la ligne d’action, passant par le centre de résistance de ce corps.

Le moment n’existe que par la force, en référence au centre de résistance. A l’équilibre, la somme des moments en présence est nulle.

I-5) Le couple

Le moment d’un couple est un vecteur libre qui produit des effets constants au niveau du centre de résistance (c’est-à-dire une rotation pure), quelle que soit la position de ce couple sur la dent. C’est un moment pur sans translation.

Un couple est un torseur obtenu par l’utilisation de deux forces :

• De même intensité
• De lignes d’action parallèles
• De sens opposés

Les deux forces s’annulent. Le moment d’un couple est égal au produit du module de l’une des composantes par la distance qui les sépare (également appelé bras de levier). Il est indépendant du point où il est pris. C’est donc un vecteur libre.

La notion du couple intervient dans les trois sens de l’espace selon LARMOLETTE.

Premier ordre : sens horizontal ou occlusal ; Une rotation disto-vestibulaire (par exemple) peut être corrigée

• Soit par l’action du moment d’une force de traction distale développée par un élastique vestibulaire. La force est ici équilibrée par la réaction de la dent proximale. Il ne subsiste que le moment par rapport au point de contact qui sert de centre de rotation.
• Soit par l’action d’un couple, composé du dispositif précédent doublé d’une force égale et opposée, sous la forme d’un élastique lingual à traction mésiale. Ici, c’est le moment du couple qui agit, et le point d’application est indifférent. La rotation se fait autour du centre de résistance.
• Soit par l’action d’un couple appliqué au niveau de la face vestibulaire (boucle). Comme précédemment, la rotation d’effectue autour du centre de résistance grâce au moment du couple.

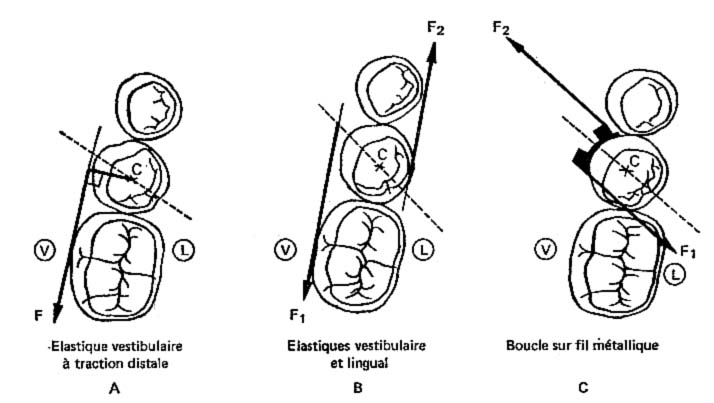
Fig. 7 : Corrections de rotation Disto-Vestibulaire : A, par moment d’une force ; B et C, Par moment d’un couple, selon Lamorlette.

Deuxième ordre : sens mésio-distal.

L’application du couple dans le sens mésio-distal permet d’effectuer le redressement des racines après fermeture des espaces, la stabilisation des ancrages (tip-back ou préparation d’ancrage), le mouvement de gression.

Troisième ordre : sens vestibulo-lingual.

L’incorporation de torque dans le fil edgewise équivaut à appliquer au niveau coronaire de chaque dent un couple dans un plan vertical vestibulo-lingual par l’intermédiaire des brackets.

I-6) Notion d’équivalence

Pour obtenir des mouvements de translation pure, l’idéal serait de travailler au centre de résistance de la dent. L’orthodontiste doit donc trouver le moyen de produire le même système de forces, ou un système équivalent sur la couronne dentaire. Les deux systèmes de forces, l’un sur la couronne de la dent et l’autre au centre de résistance, sont dit équivalents s’ils produisent les mêmes effets sur la dent.

I-7) Le rapport Force / Moment

Le rapport moment / force permet d’établir quelle sera la prédominance du mouvement vers la translation ou vers la rotation. La distance du centre de rotation par rapport au centre de résistance est donnée par l’intermédiaire du rapport Force / moment. Quel que soit le nombre de forces appliquées, le système peut toujours être ramené à une force et un moment, dont le rapport fixe le centre de rotation, et donc le type de mouvement. Pour obtenir une translation, il faut appliquer au bracket de la dent une force et un moment, sous forme de couple, pour annuler la résultante de la force au centre de résistance de la dent.

Nous avons donc en présence :

• La force
• Le moment qui en résulte (effet indésirable)
• Le moment ajouté pour le contrer.

Au fur et à mesure du déplacement, le moment ajouté reste constant, tandis que la force diminue, et avec elle le moment qu’elle engendre. Le mouvement ne se fait plus en translation, puisqu’il y a déséquilibre. Le meilleur moyen d’assurer un rapport Force / Moment constant est d’utiliser la force la plus constante possible, soit en :

• Utilisant un alliage le plus élastique possible
• Choisissant des points d’attache les plus éloignés possible
• Augmentant la longueur du fil par des boucles, c’est-à-dire en abaissant le rapport charge-fléxion des ressorts en gardant une charge maximum élevée.

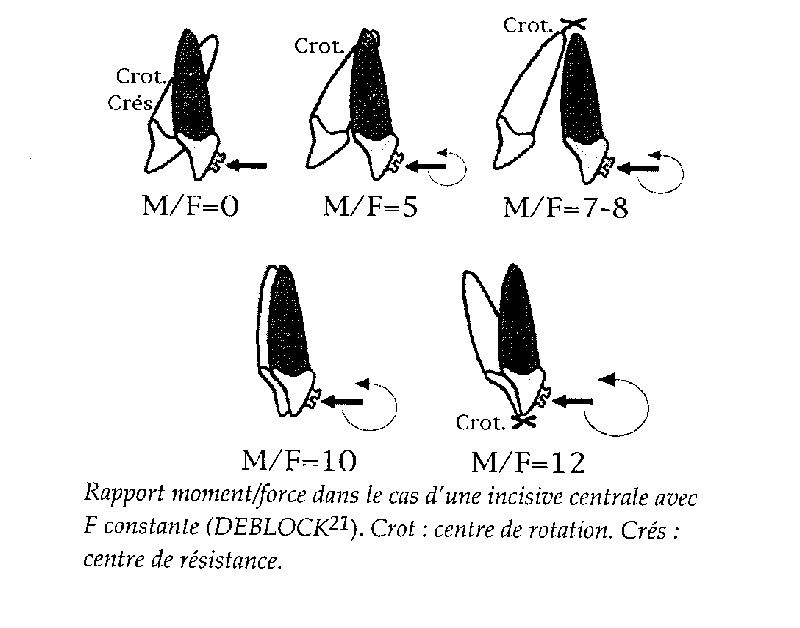
D’après les travaux de BURSTONE, pour une incisive centrale sup, chaque rapport M/F ( moment/force), entraîne un type de mouvement différent.

Translation : M/F = 10mm

Version contrôlée : M/F = 5mm ; (mouvement dont le centre instantané de rotation est situé à l’apex).

Mouvement de racine : M/F = 12 mm ; (mouvement dont le centre instantané de rotation est situé au niveau du bord libre).

Version incontrôlée autour du centre de rotation et du CR qui sont confondus : M/F= 0mm.

1. LE MOUVEMENT DENTAIRE :

II-1) Notion d’ancrage

D’après la troisième loi de NEWTON (in MARCOTTE) : tout solide qui sert d’ancrage à une force destinée à déplacer un corps libre subit également une force égale et de sens opposé, qui a tendance à entraîner ce solide en direction de la traction. En biomécanique orthodontique l’ancrage est la résistance d’un corps au déplacement. L’action engendre la réaction.

À partir d’un certain seuil, l’ancrage est insuffisant et le solide constituant l’ancrage est entraîné en direction du corps libre à déplacer.

Dans un déplacement dentaire provoqué, l’action orthodontique dépend du trinôme suivant :

• • La structure dentaire à déplacer : le mobile.
  • La structure d’appui : le stabile ou ancrage.
  • L’élément moteur.

Le mobile est caractérisé par le seuil d’intensité de force à partir duquel il commence à se déplacer. Ce seuil est la résistance mobile = RM.

De même, le stabile est caractérisé par le seuil d’intensité de force à partir duquel il commence à se déplacer. Ce seuil est la résistance stabile = RS.

La force motrice = FM caractérise l’élément moteur.

La résistance stabile peut être constituée par une ou plusieurs dents pour permettre le mouvement dentaire d’une canine par exemple, ou d’une arcade lors de tractions élastiques intermaxillaires. C’est là qu’intervient la notion d’ancrage réciproque ou de forces différentielles.

C’est la valeur réciproque des résistances qui commande le déplacement suivant le trinôme de DE NEVREZE.

Trois cas sont possibles :

• La résistance stabile est égale à la résistance mobile (ancrage réciproque) :

– si FM < (RS = RM) → il n’y a pas de déplacement.

– si FM > (RS = RM) → déplacement égal et symétrique, le mobile et la stabile se déplacent, il y a perte d’ancrage réciproque.

• La résistance stabile est plus grande que la résistance mobile :

– si FM < RM < RS → il n’y a pas de déplacement.

– si RM < RS < FM → déplacement double et inégal. La résistance mobile se déplace davantage que la résistance stabile, mais il y a cependant perte d’ancrage.

– si RM < FM < RS → déplacement orthodontique correcte désiré, sans « perte d’ancrage », seul le mobile se déplace.

• La résistance stabile est plus petite que la résistance mobile :

– si RS < RM < FM → la résistance stabile (la dent d’ancrage) se déplace plus que le mobile à déplacer. Il y a donc perte d’ancrage.

II-1-1) L’ancrage passif

Il est constitué par la dent elle-même. Celle-ci est « ancrée » dans l’os alvéolaire par l’intermédiaire du desmodonte et sa résistance au déplacement est définie par la longueur, le nombre ou le volume de ses racines, mais également par la qualité du parodonte sous-jacent.

II-1-2) L’ancrage actif

C’est l’ancrage mécanique produit par les dispositifs orthodontiques pour éviter le déplacement des dents d’appui.

Parmi ces moyens on distingue :

• Les courbures anti-version, anti-rotation des arcs,
• Les butées ou stop sur les arcs,
• Les ligatures de plusieurs dents pour additionner les valeurs d’ancrage,
• Les élastiques utilisés de façon différentielle pour éviter le déplacement des dents d’ancrage,
• Les arcs palatins, linguaux,
• Les forces extra-buccales.

Etc…

II-2) Rappel des systèmes de forces utilisés en orthodontie

Le premier système est celui d’une force simple, unique, s’appuyant sur la couronne de la dent.

Ce type de force est créé par les fils ronds des appareillages multibagues, agissant seuls sans arc auxiliaire.

Il est également provoqué par tous les dispositifs actifs installés sur les appareillages amovibles.

Le deuxième système de forces est représenté par un couple, c’est-à-dire l’association de deux forces égales, parallèles et de sens opposés. En pratique, ce système peut être mis en place sur des appareillages amovible ou fixe. Il est réalisé à l’aide de :

• Deux ressorts,
• Deux élastiques agissants en direction opposée,
• La torsion sur le chant d’un arc carré ou rectangulaire.

Le troisième système de forces est représenté par une association d’une force simple et d’un couple. En pratique, actuellement, il est cliniquement réalisable à l’aide d’appareillages fixes.

Ces trois systèmes déterminent une action qui déplacera la ou les dents de différentes manières.

II-3) Les différents types de mouvement dentaires

II-3-1) Mouvement de version contrôlée

Elle correspond à la bascule d’une dent autour d’un centre de rotation situé au niveau de son apex.

C’est le type de mouvement qui s’effectue lorsqu’une force et un moment sont appliqués sur la couronne, déplaçant la couronne dans une direction et avec un moment suffisant pour empêcher le mouvement de la racine en direction opposée.

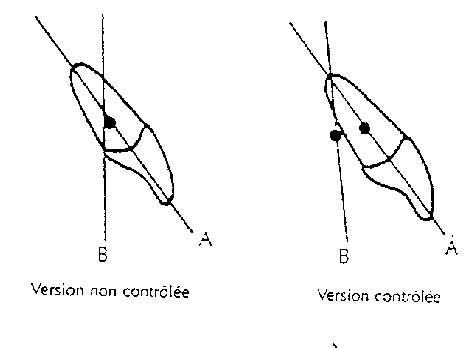
Mouvements de version selon Marcotte

II-3-2) Mouvement de racine ou de redressement après version

C’est un mouvement assez voisin de la version, mais la couronne est stabilisée, et l’apex seul fait une version. Nécessaire pour redresser l’axe de la dent versée, il s’applique au cours du mouvement de torque, ou lors de la fermeture d’un espace d’extraction.

Mouvement de redressement d’axe, d’après Langlade (Vue sagittale)

II-3-3) Mouvement de translation

Il ne peut être obtenu que si la dent porte un attachement rigide. C’est un mouvement parallèle à l’axe de la dent.

La racine se déplace exactement de la même distance que la couronne. Elle a lieu quand le centre de rotation de la dent est situé à l’infini. Tous les points de la dent se déplacent selon des droites parallèles dans la direction de la force. Selon BURSTONE, lorsqu’une dent se déplace en translation, une force de distribution relativement uniforme se répand le long de la racine. Mécaniquement, le mouvement de translation se fait grâce à l’application d’une force et d’un moment sur la dent à déplacer. Le mouvement de translation pure est possible si un rapport FORCE / MOMENT approprié à la dent. Une légère erreur de ce rapport déplacera le centre de rotation, produisant une version.

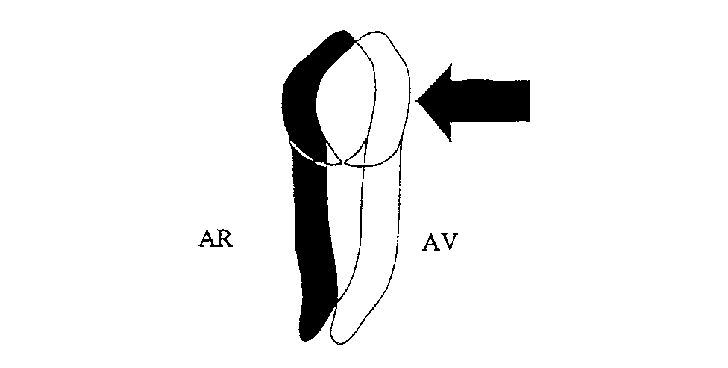
Mouvement de translation, d’après Langlade. Vue sagittale.

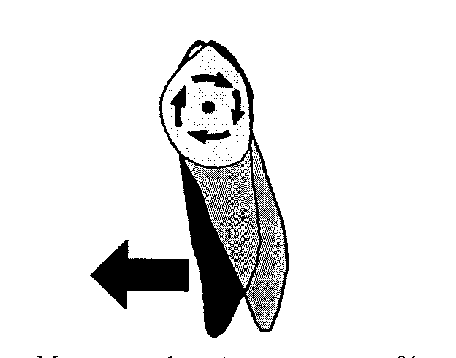
II-3-4) Mouvement de rotation (sens horizontal)

La dent tourne sur son grand axe sous l’action d’un couple. Une rotation s’effectue quand le centre de rotation est sur l’axe vertical de la dent.

II-3-5) Mouvement d’ingression (sens vertical)

C’est un changement de relation d’une dent par rapport à l’os voisin, obtenu par un mouvement de réimplantation de la dent dans l’alvéole. Ce mouvement dentaire a lieu selon une direction axiale et son centre de rotation est à l’infini.

Ces mouvements dentaires ont été décrits comme ayant lieu sur une seule dent. Mais un groupe de dents rigidement associées peut se déplacer avec son propre sens de rotation. Chaque arcade segmentée de cette façon peut être assimilée à trois « grandes dents » (BURSTONE cité par MARCOTTE), simplifiant la mécanique.

1. Système mécanique et déplacement

Il est impossible de travailler directement au niveau du centre de résistance des dents à déplacer. C’est pourquoi ont été mis au point des systèmes permettant de reproduire le même système de force, mais appliqué au niveau de la couronne.

III-1) Les attachements

Il s’agit d’un dispositif métallique, céramique ou plastique, pourvu d’une gorge dans laquelle pourra s’insérer un arc. Cet attachement est fixé directement sur la dent soit par collage, soit soudé à une bague qui est scellée, et positionné en fonction des normes (distance par rapport au sommet des cuspides ou au bord libre des incisives). C’est par cette gorge que sont transmises au niveau dentaire les informations imprimées à l’arc.

Dans les techniques d’arc droit, on a imaginé pré-programmer au niveau de la gorge des attachements toutes les informations nécessaires à la mise en place d’un arc plat et de forme régulière, afin de faciliter le travail des orthodontistes.

Ce système permet donc l’application de force aux éléments dentaires mais à distance de leur centre de résistance : c’est pourquoi il faut parler de systèmes de forces équivalents. Ce dernier implique la connaissance des effets des forces appliquées au niveau de l’attachement ainsi que du moment qu’elles impliquent. De la sorte, il faut au niveau de l’attachement appliquer, en plus de la force nécessaire à l’obtention du déplacement, un moment qui contrebalancera l’effet de l’application de la force à distance du centre de résistance de la dent à déplacer.

III-2) Les arcs

Ils sont constitués de fil métallique, et les déplacements sont induits par les déformations plastiques de l’arc ou maintenant par la lecture par l’arc des informations programmées dans les attachements.

Les paramètres du système dépendent :

• Du module d’élasticité (différent selon l’alliage étudié)

Il s’agit d’une propriété inhérente à la composition du fil. Avant l’apparition des alliages à mémoire de forme, le module d’élasticité des arcs en acier était d’avantage considéré comme une constante. On jouait iniquement sur la longueur du fil. Dorénavant, l’utilisation de l’effet mémoire de forme permettra l’application de forces légères et continues (à moduler par variations de température).

Module élevé (ressort rigide)=A ; module bas (ressort flexible)=B, d’après Marcotte

• Du moment d’inertie (fonction de la section du fil)

Il caractérise la rigidité des fils, en fonction de la section de ces fils : au niveau atomique, la mise en flexion provoque une compression des fibres les plus basses et une élongation des fibres les plus hautes, les fibres moyennes restant neutres. De ce fait, plus la section est importante, plus le fil est rigide.

Les fils tressés permettent de diminuer la raideur des fils sans changer la section (le rapport charge / flexion variant proportionnellement avec le nombre de brins contenu dans la tresse).

Les fils rectangulaires tressés autorisent également la lecture des informations dans tous les sens de l’espace, tout en gardant leur souplesse.

• De la longueur utile du fil entre les attachements.

Elle influence directement le rapport charge / Flexion. Cette propriété est utilisée lors de l’adjonction de boucles sur un arc. La forme et la disposition des boucles sont fonction des déplacements à réaliser.

III-3) Les mécanismes :

III-3-1) L’appareillage de base :

L’arc et les attachements constituent le mécanisme, qui provoque les mouvements dentaires. Ils permettent la transformation « d’énergie mécanique en déplacement dentaire »

La forme idéale des arcs serait « celle d’un fil rond pour une activation multiplan», pour Langlade, mais ce type de fil ne permet pas un contrôle du torque (troisième ordre), le fil rectangulaire paraît le plus indiqué.

Pour obtenir une force constante, il n’existe pour Duhart et Coll. Qu’un moyen : Utiliser un mécanisme que l’on pourra activer bien au-delà du déplacement à obtenir. Cela implique un type de fil (choisi pour son rapport charge / flexion faible) et un rapport activation / déplacement le plus élevé possible.

III-3-2) Les auxiliaires :

Ce sont des dispositifs annexes permettant de délivrer ces forces supplémentaires aidant au déplacement ou à la préservation de l’ancrage.

Ils comprennent entre autres :

• Les chaînettes élastomériques,
• Les ressorts (acier, nickel-titane, serrés ou ouverts),
• Les élastiques de traction intermaxillaires,
• Les forces extra-orales,
• Les éléments intra-buccaux de préservation d’ancrage : pastille de Nance, arc transpalatin, arc lingual, etc …

III-4) Relations entre arcs et les attaches

Nous nous efforcerons dans ce paragraphe d’expliciter les réactions de dents voisines à une courbure d’activation, ceci en passant sous silence les actions des forces transmises à distance, dans un souci de simplification.

III-4-1) Le V symétrique

Étant donnée la courbure de l’arc par rapport aux attaches, il existe 4 forces en présence, qui répondent aux conditions d’équilibre statique. (Ce dernier étant régi par la troisième loi de Newton).

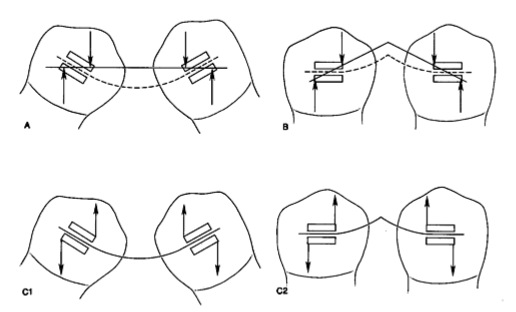
A : 2 couples agissant à chaque extrémité de l’arc. Quand un arc droit est placé dans des attaches en rotation, l’arc doit être déformé par 2 couples égaux et opposés agissant sur les extrémités de l’arc. La ligne continue représente la forme initiale de l’arc et la ligne discontinue, l’arc après déformation. B, la même combinaison de couples décrite en A est nécessaire pour placer un arc avec une courbure en V permanente, dont la pointe est centrée entre les attaches. C, les forces agissent sur les dents par l’élasticité de l’arc tel qu’il a été déformé en A ou B.

Pour répondre aux conditions de l’équilibre statique, il faut que chaque force des couples soit d’amplitude égale. Ainsi, la somme des forces verticales et horizontales est nulle et les moments des forces s’annulent deux à deux.

L’arc va donc travailler en se désactivant et provoquer une rotation des dents en sens inverse. Une courbure centrée ne crée donc pas de force mais des moments égaux et opposés.

III-4-2) Le V asymétrique

Dans ce cas, la courbure est décentrée et crée un système complexe de forces et de moments.

Au niveau des forces, on obtiendra des forces égales et opposées, avec le segment long pointant dans la direction de la force produite et le segment court dans la direction opposée.

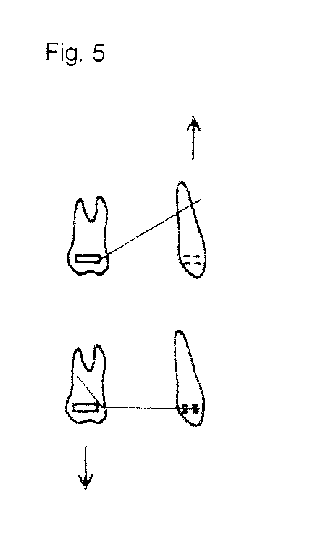
Les moments de ces forces sont par contre inégaux, le moment le plus important étant situé sur l’attache contenant le segment le plus court. En jouant sur l’angulation de l’arc et des attaches, le petit moment donné par le segment long, pourra être positif, négatif ou nul.

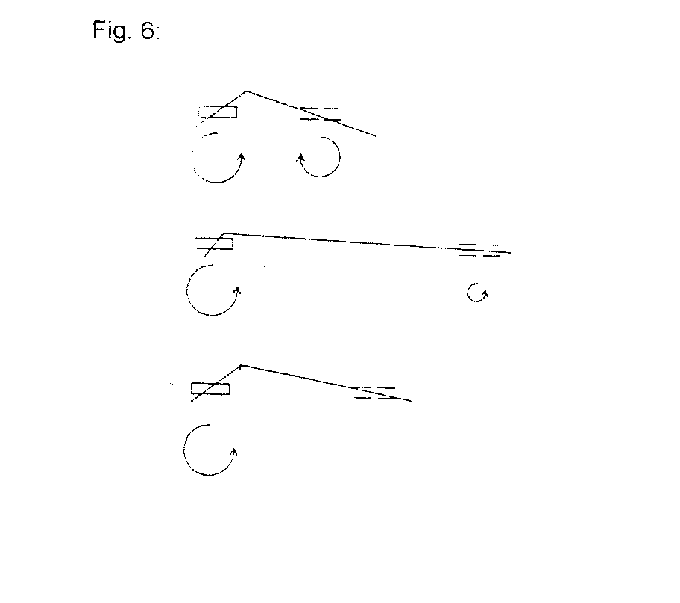
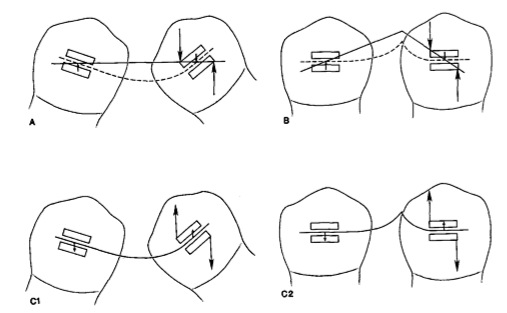
A, 2 couples, l’un placé à l’extrémité de l’arc et l’autre placé le long de celui-ci. Ces couples sont nécessaires pour placer un arc droit dans des attaches non alignées. (L’attache de gauche est en rotation de moitié par rapport à l’attache de droite et de sens opposé). B, Les mêmes couples décrits en A sont nécessaires pour placer le fil avec la courbure en V située au tiers de la distance inter-bracket. C, le système de force de ces 2 arcs (A et B) est identique.

III-4-3) La relation en escalier

Dans ce système, seule la figure 8 B répond aux conditions d’équilibre statique : la somme des forces verticales est nulle et il n’existe pas de forces horizontales. Les moments s’annulent deux à deux que dans la mesure où les forces A et D sont plus faibles que les forces B et C, tout en étant d’intensité identique et de force de direction opposée (ceci s’explique par le fait que A et D sont appliquées à une plus grande distance du centre que B et C).

A cette condition, on observera une bascule des dents, toutes les deux dans le même sens.

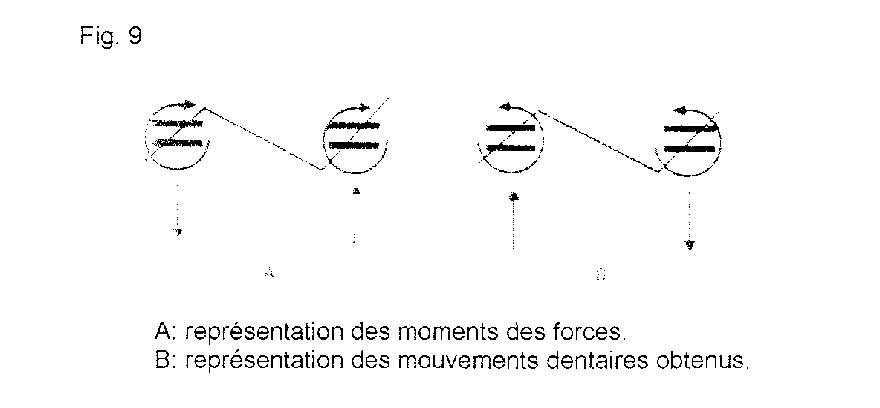
Pour Mulligan, la connaissance de ces relations permet de simplifier et de rationaliser les appareillages.

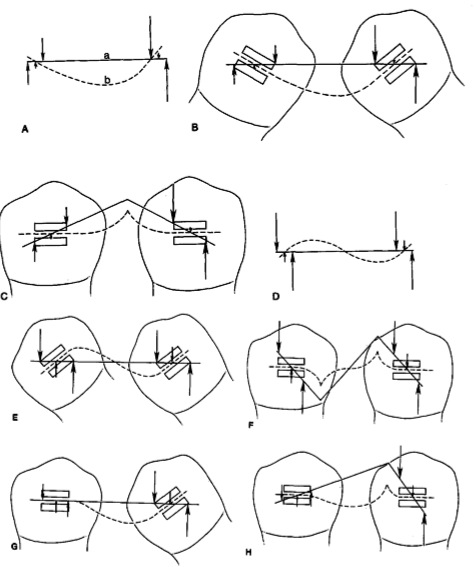
A, les forces de trois couples peuvent être en l’équilibre. Si deux couples agissant sur les extrémités opposées du fil produisent des moments de direction opposée et de grandeur différente, le fil peut être apporté à l’équilibre par un couple agissant sur toute sa longueur. B, la combinaison des couples décrits en A est nécessaire pour que le fil droit soit placé dans les attaches (l’attache de gauche est tournée de trois quarts par rapport à l’attache de droite dans la direction opposée). C, la même combinaison des couples (A et B) est exigé pour placer le fil avec la courbure en V, dont la pointe est placé entre la moitié et le tiers de la distance inter-brackets des attaches bien-alignées. D, une autre combinaison de trois couples qui peuvent avoir comme conséquence l’équilibre. Deux couples agissant sur de courtes étendues aux extrémités du fil produisent tous deux la rotation du fil dans la même direction. Ils sont équilibrés le couples agissant sur toute la longueur du fil qui produit la rotation dans la direction opposée. E, le système de force décrit en D est exigé pour que le fil droit soit placé dans deux attaches qui sont tournées dans la même direction et de même angulation à partir de l’axe d’interbracket. F, placer le fil avec la courbure en escalier dans deux attaches bien-alignées exige le même système de force décrit par l’exemple D, placer le fil droit dans deux attaches, dont une est alignée avec l’axe d’interbracket alors qu’autre ne l’est pas, exige essentiellement le même système de force (bien que l’importance de forces peut être quelque peu différente). H, le même système de force vu en G est exigé pour placer le fil à courbure en V, dont la pointe est placée à moins du tiers de la distance d’une attache à autre.

CONCLUSION 

Au cours des traitements orthodontiques réalisés à l’aide d’une technique fixe, le mouvement dentaire est guidé par le ou les contacts entre le fil orthodontique et l’attache. Ainsi les propriétés des arcs et des attachements ont une influence sur le déplacement des dents.

Si le système fil attache permet le contrôle des mouvements dentaires, il engendre des forces de frictions qui s’opposent au mouvement souhaité. Ainsi, l’étude mécanique du mouvement dentaire guidé par un fil orthodontique fait appel aux lois de frottement.

Les progrès actuels réalisés en orthodontie sont presque toujours liés :

• À l’amélioration des attaches, des fils, notamment avec des traitements de surface, ainsi que les nouveaux systèmes de ligatures visant à diminuer la friction, et des fils aux qualités physiques accrues.
• À une meilleure compréhension des mécanismes précédant au déplacement dentaire provoqué.
• À une connaissance approfondie des phénomènes de croissance et de l’équilibre fonctionnel des patient.

BIBLIOGRAPHIE :

1. ALOE Ph .

Les forces extra-buccales appliquées sur les molaires supérieures

Dix questions d’orthopédie Dento-faciale, deuxième série,

Paris : J. Prélat, 1971, 89-111

2. ALTOUNIAN G.

Biomécanique des forces extra-buccales dans le sens sagittal

Dix questions d’orthopédie Dento-faciale, troisième série,

Paris : J. Prélat, 1975, 87-99

2 Bis. AUGE F., MAURAN F., PARGUEL P.

Principes mécaniques de la technique BEGG

Orthop. Fr., 1979, 50, 317-328

3 . BARIL C.

Biomechanics.

Montréal: université de Montréal, 1970

4. BASSIGNY F.

Manuel d’orthopédie Dento-Faciale, 2^ème éd.

Paris : Masson, 1991

5. BENAUWT A.

Au delà de la mécanique, et un certain état d’esprit

Rev. Ortho. Dentofac., 1988, 22, 121-127

6. BEQUAIN D., DARQUE J., PUJOL A.

Rapport charge/ flexion et rapport activation/déplacement dans la conception des mécanismes orthodontiques

Orthop. Fr., 1956, 57, 823-831

7. BECQUAIN, D.

Réflexions sur le trinôme de De Névrezé

Orthod Fr, 1993, 64, 2, 533-544.

8. BONNEFONT R., GUYOMARD F.

Rappel des notions de mécaniques utilisables en O.D.F

Rev. Orthop. Dentofac., 1979, 13, 5-25

9. BURSTONE C.J

Biomechanics of the orthodontic appliance, 160-178

In: Current orthodontic and techniques, vol.1 Ed T.M. GRABER

10. CALOP M.P.

Biomécanique en orthodontie : applications pratiques

Mémoire de CECSMO 1997

11. CHATEAU M

Orthopédie Dento-Faciale, vol. 2

Paris: Ed. CdP, 1993

12. FURSTMAN, BERNICK et ALDRICH

Differential response incident to tooth movement

Am. J. Orthod. , 1971, 59, 541-551

13. GARCIA R.

Biomécanique de l’arc continu

Orthop. Fr., 1990, 61, 437-457

14. HIXON EH., ATIKIAN H., CALLOW GE., Mc DONALD et TACY RJ

Optimal force, differential force et anchorage

Am. J. Orthod. 1969, 55, 437-457

15. HIXON E.H., AASEN TO., ARANGO J., CLARK RA.

On force and tooth movements

Am. J. Orthod. 1970, 57, 476-488

16. KUHLBERG A.J., NANDA R

Applications des concepts biomécaniques à la clinique orthodontique

Rev. Orthop. Dentofac., 1994, 28, 325-334

17. LANGLADE M.

Thérapeutique orthodontique

Maloine s.a éditeur paris, 1986.

18. LAMORLETTE D .

Notions fondamentales de biomécanique

Dix questions d’orthopédie dento-faciale, troisième série, J. Prélat, 1975.

19. MARCOTTE M. Biomécanique en Orthodontie. Paris: Ed. CdP, 1995, 178.

20. SHELHART CW.

Equilibrium clarified.

AJODO, 1995, 108 : 394-401.

21)TEUSCHER U.

An appraisal of growth and reaction to extra-oral anchorage

AJO, 89 : 113-121, 1986.

22) VION P.

Les fascicules de l’orthodontie : Biomécanique

Editions S I D, 2000.